Photon Targets for External Compton
The classes here described will provide the targets for the external Compton scattering. They also allow, in the case of the accretion disk and dust torus, to compute their own black-body radiative emission.
The following objects are implemented:
CMB, representing the Cosmic Microwave Background;PointSourceBehindJet, representing a monochromatic point source behind the jet. This is mostly used to crosscheck that the energy densities and external Compton SEDs of the other targets reduce to this simplified case for large enough distances ([Dermer1994], [Dermer2002]);SSDisk, representing a [Shakura1973] (i.e. a geometrically thin, optically thick) accretion disk;SphericalShellBLR, representing the broad line region (BLR) as an infinitesimally thin spherical shell, on the lines of [Finke2016];RingDustTorus, representing the dust torus (DT) as an infintesimally thin ring, see treatment of [Finke2016].
Shakura Sunyaev disk
The accretion disk can be intialised specifying:
the mass of the central Black Hole, \(M_{\mathrm{BH}}\);
the disk luminosity, \(L_{\mathrm{disk}}\);
the efficiency to transform accreted matter to escaping radiant energy, \(\eta\);
the inner and outer disk radii, \(R_{\mathrm{in}}\) and \(R_{\mathrm{out}}\).
import numpy as np
import astropy.units as u
import astropy.constants as const
from agnpy.targets import SSDisk
# quantities defining the disk
M_BH = 1.2 * 1e9 * const.M_sun
L_disk = 2 * 1e46 * u.Unit("erg s-1")
eta = 1 / 12
R_g = 1.77 * 1e14 * u.cm
R_in = 6 * R_g
R_out = 200 * R_g
disk = SSDisk(M_BH, L_disk, eta, R_in, R_out)
Alternatively the disk can be initialised specifying R_in and R_out in dimensionless units of gravitational radius, setting the
R_g_units argument to True (False by default).
# alternative initialisation using gravitational radius units
disk = SSDisk(M_BH, L_disk, eta, 6, 200, R_g_units=True)
print(disk)
* Shakura Sunyaev accretion disk:
- M_BH (central black hole mass): 2.39e+42 g
- L_disk (disk luminosity): 2.00e+46 erg / s
- eta (accretion efficiency): 8.33e-02
- dot(m) (mass accretion rate): 2.67e+26 g / s
- R_in (disk inner radius): 1.06e+15 cm
- R_out (disk inner radius): 3.54e+16 cm
Broad Line Region (BLR)
The BLR can be initialised specifying:
the luminosity of the disk whose radiation is being reprocessed, \(L_{\mathrm{disk}}\);
the fraction of radiation reprocessed, \(\xi_{\mathrm{line}}\);
the type of line emitted (for a complete list see the
print_lines_list()function);the radius at which the line is emitted, \(R_{\mathrm{line}}\).
Let us continue from the previous snippet considering a BLR reprocessing the previous disk luminosity and re-emitting the \(\mathrm{Ly}\alpha\) line:
from agnpy.targets import SphericalShellBLR
# quantities defining the BLR
xi_line = 0.024
R_line = 1e17 * u.cm
blr = SphericalShellBLR(L_disk, xi_line, "Lyalpha", R_line)
print(blr)
* Spherical Shell Broad Line Region:
- L_disk (accretion disk luminosity): 2.00e+46 erg / s
- xi_line (fraction of the disk radiation reprocessed by the BLR): 2.40e-02
- line (type of emitted line): Lyalpha, lambda = 1.22e-05 cm
- R_line (radius of the BLR shell): 1.00e+17 cm
Dust Torus (DT)
The DT can be initialised specifying:
the luminosity of the disk whose radiation is being reprocessed, \(L_{\mathrm{disk}}\);
the fraction of radiation reprocessed, \(\xi_{\mathrm{dt}}\);
the temperature at which the black-body radiation peaks, \(T_{\mathrm{dt}}\);
the radius of the ring representing the torus, \(R_{\mathrm{dt}}\). The latter is optional and if not specified will be automatically set at the sublimation radius (Eq. 96 in [Finke2016]).
Let us continue from the previous snippet considering a DT reprocessing the disk luminosity in the infrared (\(T_{\mathrm{dt}} = 1000 \, \mathrm{K}\)):
from agnpy.targets import RingDustTorus
# quantities defining the DT
T_dt = 1e3 * u.K
xi_dt = 0.1
dt = RingDustTorus(L_disk, xi_dt, T_dt)
print(dt)
* Ring Dust Torus:
- L_disk (accretion disk luminosity): 2.00e+46 erg / s
- xi_dt (fraction of the disk radiation reprocessed by the torus): 1.00e-01
- T_dt (temperature of the dust torus): 1.00e+03 K
- R_dt (radius of the torus): 1.57e+19 cm
Black-Body SEDs
The SEDs due to the black-body (BB) emission by the disk and the DT can be computed via the sed_flux method of the two classes.
A multi-temperature BB is considered for the disk and a simple single-temperature BB for the DT.
An array of frequencies over which to compute the SED and the redshift of the host galaxy have to be specified to the sed_flux function.
from agnpy.utils.plot import load_mpl_rc, plot_sed
import matplotlib.pyplot as plt
# redshift of the host galaxy
z = 0.1
# array of frequencies to compute the SEDs
nu = np.logspace(12, 18) * u.Hz
# compute the SEDs
disk_bb_sed = disk.sed_flux(nu, z)
dt_bb_sed = dt.sed_flux(nu, z)
# plot them
load_mpl_rc()
fig, ax = plt.subplots()
plot_sed(nu, disk_bb_sed, lw=2, label="Accretion Disk")
plot_sed(nu, dt_bb_sed, lw=2, label="Dust Torus")
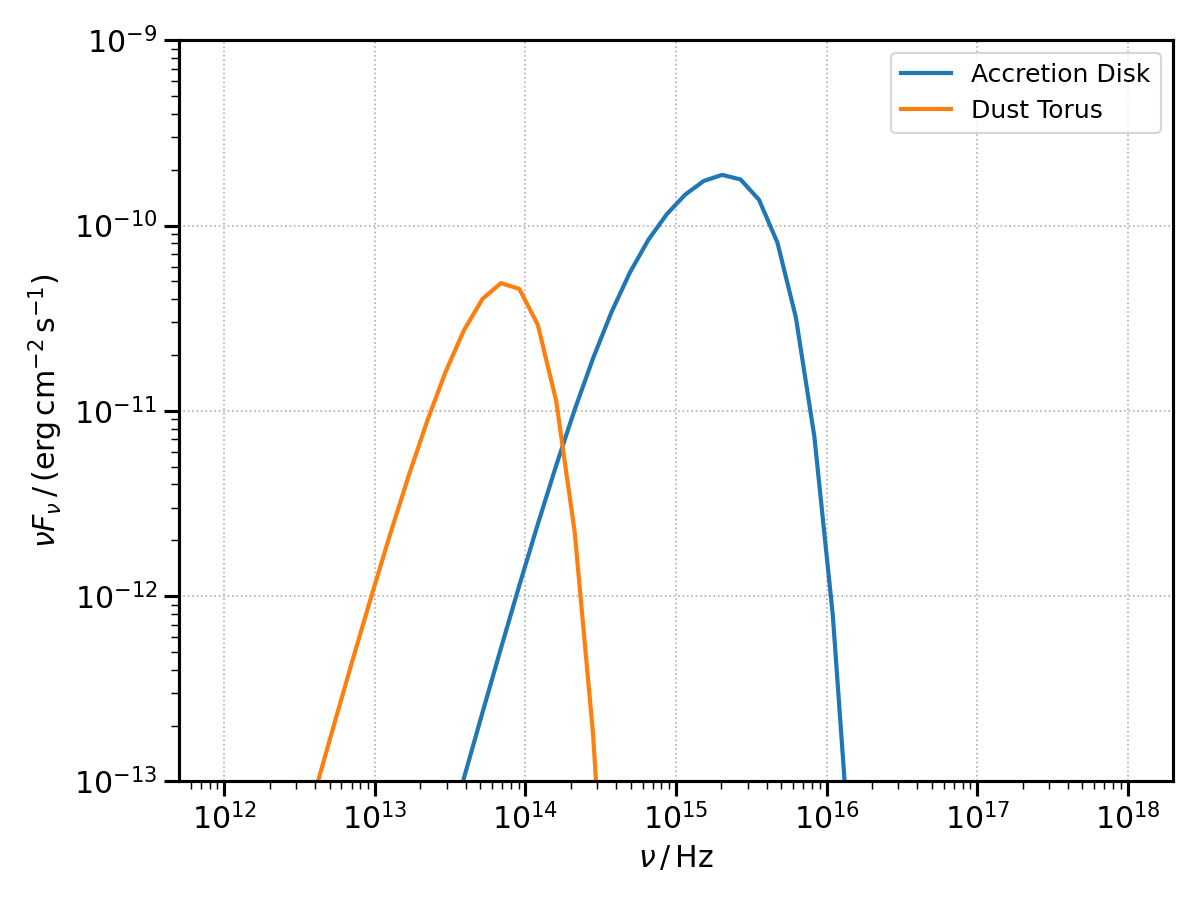
NOTE: the BB emission of the thermal components is mostly meant to check their flux levels against that of the non-thermal ones. In this notebook we illustrate that the BB emission of the DT might not be sufficiently accurate to reproduce its \(100 - 1\,{\mathrm{\mu m}}\) SED.
Energy densities
agnpy allows also to compute the energy densities produced by the photon targets,
check the tutorial notebook on energy densities.